Material Size Dependence on Fundamental Constants
Lukáš F. Pašteka, 1, 2, 3 Yongliang Hao,4 Anastasia Borschevsky,4 Victor V. Flambaum,5, 2 and Peter Schwerdtfeger2, 3
1Department of Physical and Theoretical Chemistry, Faculty of Natural Sciences, Comenius University, Mlynská dolina, 84104 Bratislava, Slovakia
2Centre for Theoretical Chemistry and Physics, The New Zealand Institute for Advanced Study, Massey University Auckland, Private Bag 102904, 0745 Auckland, New Zealand
3Centre for Advanced Study at the Norwegian Academy of Science and Letters, Drammensveien 78, NO-0271 Oslo, Norway
4Van Swinderen Institute for Particle Physics and Gravity, University of Groningen, Nijenborgh 4, 9747 AG Groningen, The Netherlands
5School of Physics, University of New South Wales, Sydney 2052, Australia
Several unification theories and standard model (SM) extensions predict variation of fundamental constants (VFC) in space and in time [1]. It has also been hypothesized that interaction of ordinary matter with a scalar dark matter (DM) field can produce temporal drifts or oscillations in the values of the fundamental constants [2], while topological defects in the DM field can produce transient VFC [3]. A typical route to observe such effects is through systematic measurements of transitions in atomic/molecular spectra sensitive to the variation of dimensionless fundamental quantities such as the fine structure constant α = e2/ ℏc or the proton-to-electron mass ratio µ = mp/me [4].
Laser interferometers now reach precision far exceeding that of any spectroscopic apparatus and thus offer a new promising direction in the search for VFC [5]. This line of research is directly connected to the dependence of material size on VFC, through the use of resonant-mass detectors [6] or cryogenic sapphire and silicon oscillators [7]. In order to interpret such experiments, knowledge of dependence of the crystal size on the fundamental constants is needed.
In this work we present a systematic investigation of the variation of crystal lattice parameters (ae and ce) and molecular bond lengths ( Re ) due to variation of the fine structure constant and the proton-to-electron mass ratio for selected solid state and molecular systems.
Precision interferometry can now provide relative sensitivity of parameters such as δL/L to VFC beyond that of any other physical apparatus. Combining this with the calculated fractional variation of crystal sizes and the use of silicon, sapphire or other single crystal oscillators or optical cavities offers a new path to testing VFC and search for scalar low-mass dark matter beyond the most stringent limits.
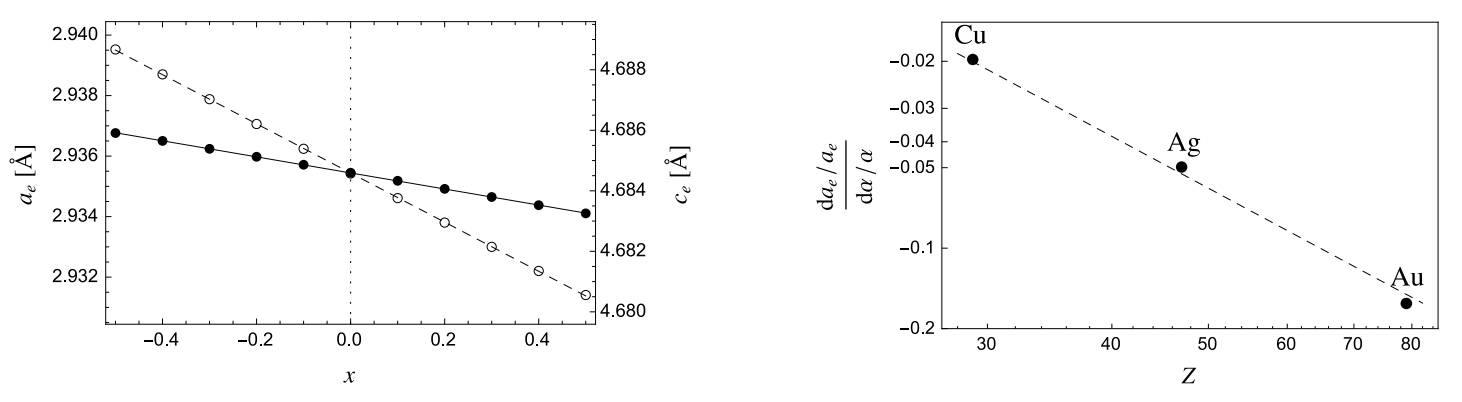
FIG. 1. Left: Dependence of the lattice constants ae, ce (full and open circles, respectively) of bulk Ti on the relativistic parameter x = (α/α0)2 − 1. Right: Z-scaling of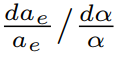 
for group 11 elements. Dashed line shows the ideal Z2 fit.
[1] J.-P. Uzan, “Varying constants, gravitation and cosmology,” Living Rev. Relativity 14, 2 (2011)
[2] Y. V. Stadnik and V. V. Flambaum, “Can dark matter induce cosmological evolution of the fundamental constants of nature?” Phys. Rev. Lett. 115, 201301 (2015)
[3] A. Derevianko and M. Pospelov, “Hunting for topological dark matter with atomic clocks,” Nature Phys. 10, 933 (2014)
[4] L. F. Pašteka, A. Borschevsky, V. V. Flambaum, and P. Schwerdtfeger, “Search for the variation of fundamental constants: Strong enhancements in X 2Π cations of dihalogens and hydrogen halides,” Phys. Rev. A 92, 012103 (2015)
[5] Y. V. Stadnik and V. V. Flambaum, “Enhanced effects of variation of the fundamental constants in laser interferometers and application to dark-matter detection,” Phys. Rev. A 93, 063630 (2016)
[6] A. Arvanitaki, S. Dimopoulos, and K. Van Tilburg, “Sound of dark matter: Searching for light scalars with resonant-mass detectors,” Phys. Rev. Lett. 116, 031102 (2016)
[7] M. E. Tobar, P. Wolf, S. Bize, G. Santarelli, and V. Flambaum, “Testing local lorentz and position invariance and variation of fundamental constants by searching the derivative of the comparison frequency between a cryogenic sapphire oscillator and hydrogen maser,” Phys. Rev. D 81, 022003 (2010).